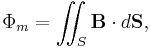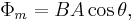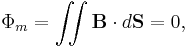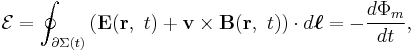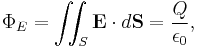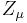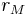Magnetic flux

Electromagnetism

Electricity · Magnetism Electrostatics Electric charge · Coulomb's law · Electric field · Electric flux · Gauss's law · Electric potential · Electrostatic induction · Electric dipole moment · Polarization density Magnetostatics Ampère's law · Electric current · Magnetic field · Magnetization · Magnetic flux · Biot–Savart law · Magnetic dipole moment · Gauss's law for magnetism Electrodynamics Free space · Lorentz force law · emf · Electromagnetic induction · Faraday’s law · Lenz's law · Displacement current · Maxwell's equations · EM field · Electromagnetic radiation · Liénard–Wiechert potential · Maxwell tensor · Eddy current Electrical Network Electrical conduction · Electrical resistance · Capacitance · Inductance · Impedance · Resonant cavities · Waveguides Covariant formulation Electromagnetic tensor · EM Stress-energy tensor · Four-current · Electromagnetic four-potential Scientists Ampère · Coulomb · Faraday · Gauss · Heaviside · Henry · Hertz · Lorentz · Maxwell · Tesla · Volta · Weber · Ørsted

Magnetic flux (Greek letter Φ (phi)), is a measure of the magnetic field strength existing on a two dimensional surface, such as one side of a magnet. In textbook diagrams, magnetic flux is usually pictured as cluster of vectors attached to a geometrically abstract surface. Each vector intersects a separate point on the surface. The SI unit of magnetic flux is the weber (in derived units: volt-seconds), and the unit of magnetic field is the weber per square meter, or tesla. (In cgs units the unit of magnetic flux is the maxwell.)

Description

Figure 1: The definition of surface integral relies on splitting the surface into small surface elements. Each element is associated with a vector dS of magnitude equal to the area of the element and with direction normal to the element and pointing outward.

Figure 2: A vector field of normals to a surface.

The flux through an element of area perpendicular to the direction of magnetic field is given by the product of the magnetic field and the area element.

More generally, the magnetic flux at any angle to a surface is defined by a scalar product of the magnetic field and the area element vector.

The direction of the magnetic field vector B is by definition from the south to the north pole of a magnet (within the magnet). Outside of the magnet, the field lines will go from north to south.

The magnetic flux through a surface is proportional to the number of magnetic field lines that pass through the surface. This is the net number, i.e. the number passing through in one direction, minus the number passing through in the other direction.

Quantitatively, the magnetic flux through a surface S is defined as the integral of the magnetic field over the area of the surface (See Figures 1 and 2):

where

is the magnetic flux

B is the magnetic field,

S is the surface (area),

denotes dot product,

dS is an infinitesimal vector, whose magnitude is the area of a differential element of S, and whose direction is the surface normal. (See surface integral for more details.)

In the special case where the surface S is a planar surface with area A, and the magnetic field is constant with magnitude B, the formula simplifies to

where θ is the angle between B and the surface normal to S.

The magnetic flux is usually measured with a fluxmeter. The fluxmeter contains measuring coils and electronics that evaluates the change of voltage in the measuring coils to calculate the magnetic flux.

Magnetic flux through a closed surface

Gauss's law for magnetism, which is one of the four Maxwell's equations, states that the total magnetic flux through a closed surface is equal to zero. (A "closed surface" is a surface without boundaries, such as the surface of a sphere or a cube, but not like the surface of a disk.) This law is a consequence of the empirical observation that magnetic monopoles have never been found.

In other words, Gauss's law for magnetism is the statement:

for any closed surface S.

Magnetic flux through an open surface

Figure 3: A vector field F ( r, t ) defined throughout space, and a surface Σ bounded by curve ∂Σ moving with velocity v over which the field is integrated.

While the magnetic flux through a closed surface is always zero, the magnetic flux through an open surface is an important quantity in electromagnetism. For example, a change in the magnetic flux passing through a loop of conductive wire will cause an electromotive force, and therefore an electric current, in the loop. The relationship is given by Faraday's law:

where (see Figure 3):

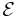is the EMF,

Φ_m is the flux through a surface with an opening bounded by a curve ∂Σ(t),

∂Σ(t) is a closed contour that can change with time; the EMF is found around this contour, and the contour is a boundary of the surface over which Φ_m is found,

dℓ is an infinitesimal vector element of the contour ∂Σ(t),

v is the velocity of the segment dℓ,

E is the electric field,

B is the magnetic field.

The EMF is determined in this equation in two ways: first, as the work per unit charge done against the Lorentz force in moving a test charge around the (possibly moving) closed curve ∂Σ(t), and second, as the magnetic flux thorough the open surface Σ(t).

This equation is the principle behind an electrical generator.

Comparison with electric flux

By way of contrast, Gauss's law for electric fields, another of Maxwell's equations, is

where

E is the electric field,

S is any closed surface,

Q is the total electric charge inside the surface S,

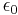is the electric constant (a universal constant, also called the "permittivity of free space").

Note that the flux of E through a closed surface is not always zero; this indicates the presence of electric "monopoles", that is, free positive or negative charges.

See also

• Magnetic field
• Maxwell's equations (sometimes called the Maxwell equations) are the set of four equations, attributed to James Clerk Maxwell, that describe the behavior of both the electric and magnetic fields, as well as their interactions with matter.
• Gauss's law gives the relation between the electric flux flowing out a closed surface and the electric charge enclosed in the surface.
• Magnetic circuit is a method using an analogy with electric circuits to calculate the flux of complex systems of magnetic components.
• Magnetic monopole is a hypothetical particle that may be loosely described as "a magnet with only one pole".
• Magnetic flux quantum is the quantum of magnetic flux passing through a superconductor.
• Carl Friedrich Gauss developed a fruitful collaboration with the physics professor Wilhelm Weber; it led to new knowledge in the field of magnetism.
• James Clerk Maxwell demonstrated that electric and magnetic forces are two complementary aspects of electromagnetism.

External articles

Patents

• Vicci, U.S. Patent 6,720,855, Magnetic-flux conduits
• Magnetic Flux through a Loop of Wire by Ernest Lee, Wolfram Demonstrations Project.